Excelでは簡単に相関関係を検証し、その結果を予想値・目標値に活用することができます。
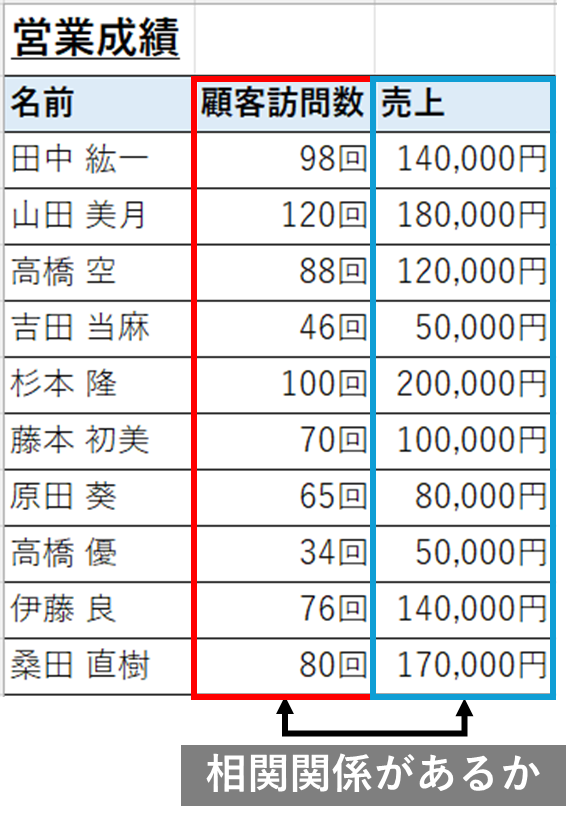
今回はこのような営業成績表に基づき、相関関係を検証します。ここでは、各担当者の顧客訪問数と売上に相関関係があるかを検証します。
2021年以降を中心にExcelに追加された機能・関数の中で特に実務に役立つものについて解説しています。基本的な使い方や他の機能・関数と組み合わせた応用テクニックも紹介しています。
コンサルタントとして様々なプロジェクトに従事してきた著者が、実務において実際に活用したExcelのテクニックを紹介します。著者自身が「あれ？どうすればいいんだろう」と悩んだ部分を中心にピックアップしています。
散布図を使った視覚的な相関関係の検証
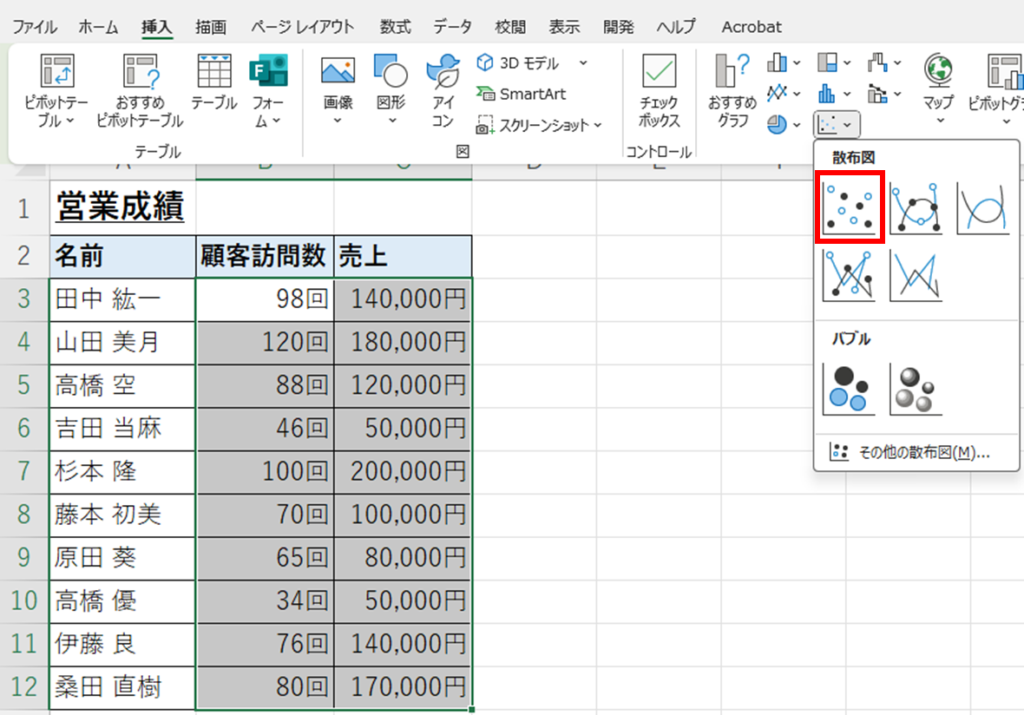
まずは散布図を使って視覚的に検証を行ってみます。顧客訪問数と売上のデータを選択し、挿入タブのグラフから散布図を選択します。
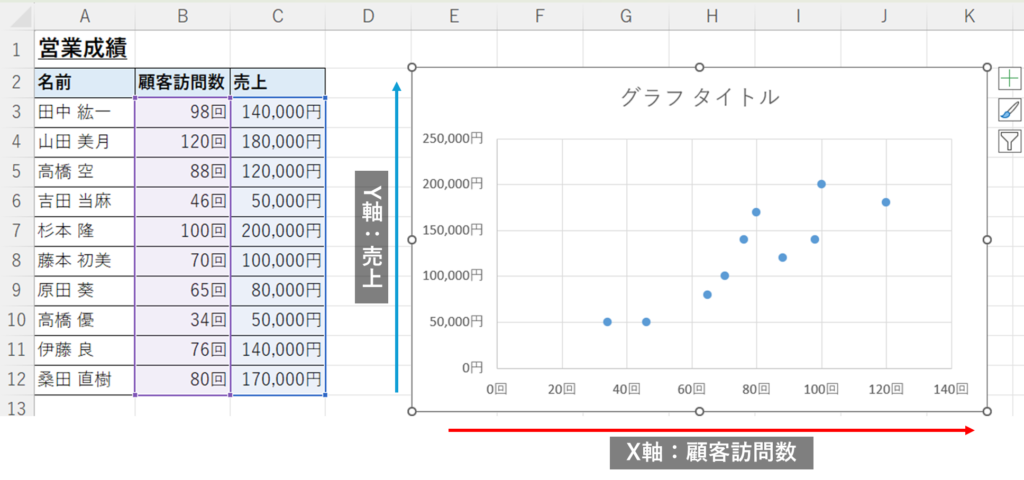
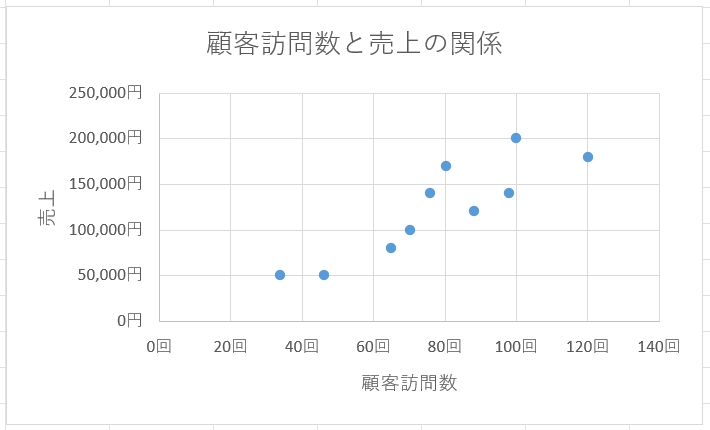
これで、X軸に顧客訪問数、Y軸に売上を持つ散布図を作成することができます。1つ1つの点は各担当者のデータを表します。
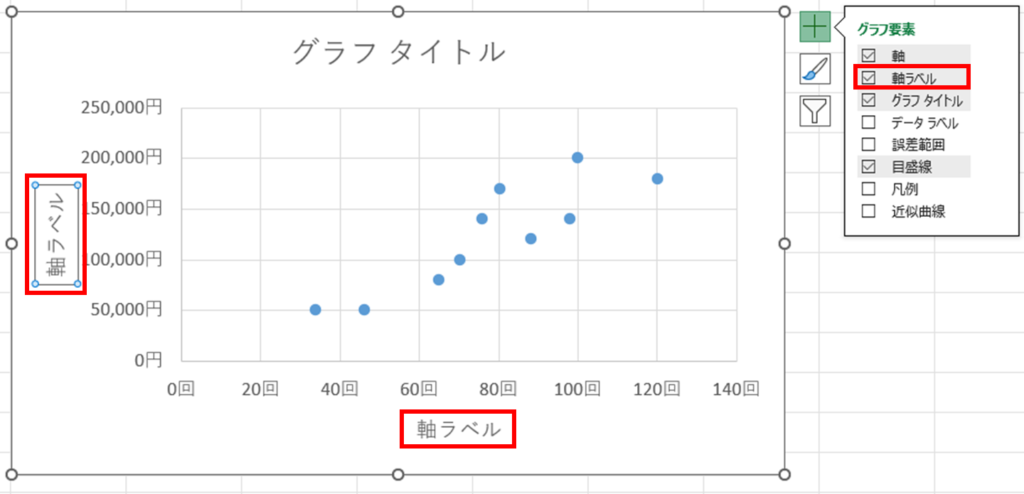
軸ラベルを追加し、タイトルとラベルを付けます。
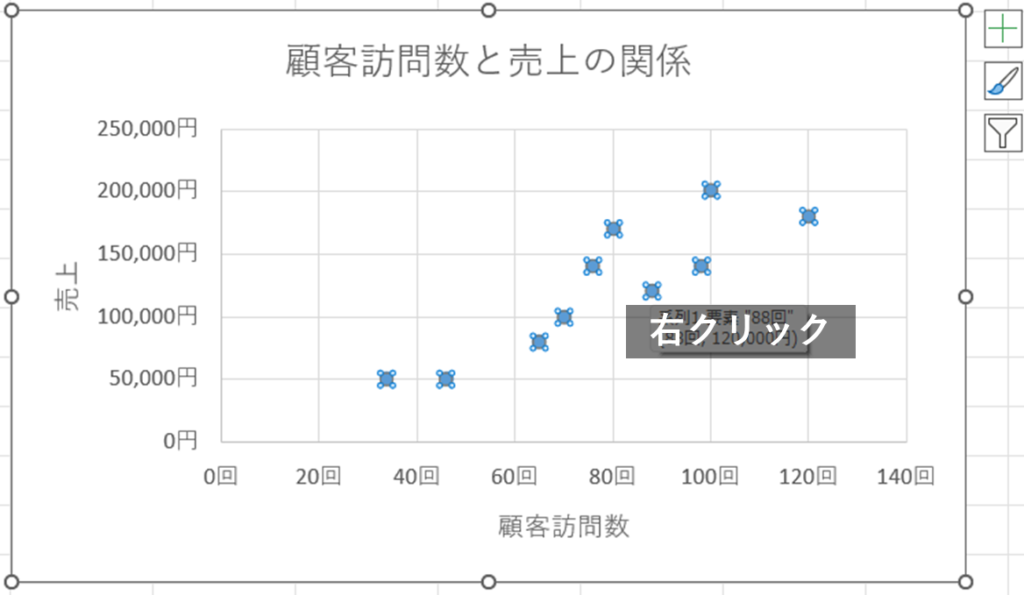
次に散布図に近似曲線を引きます。近似曲線とは散布図上にプロットされた複数のデータ点の全体的な傾向を表すために引かれる線のことを言います。散布図上の点を1回クリックし、右クリックでメニューを開きます。
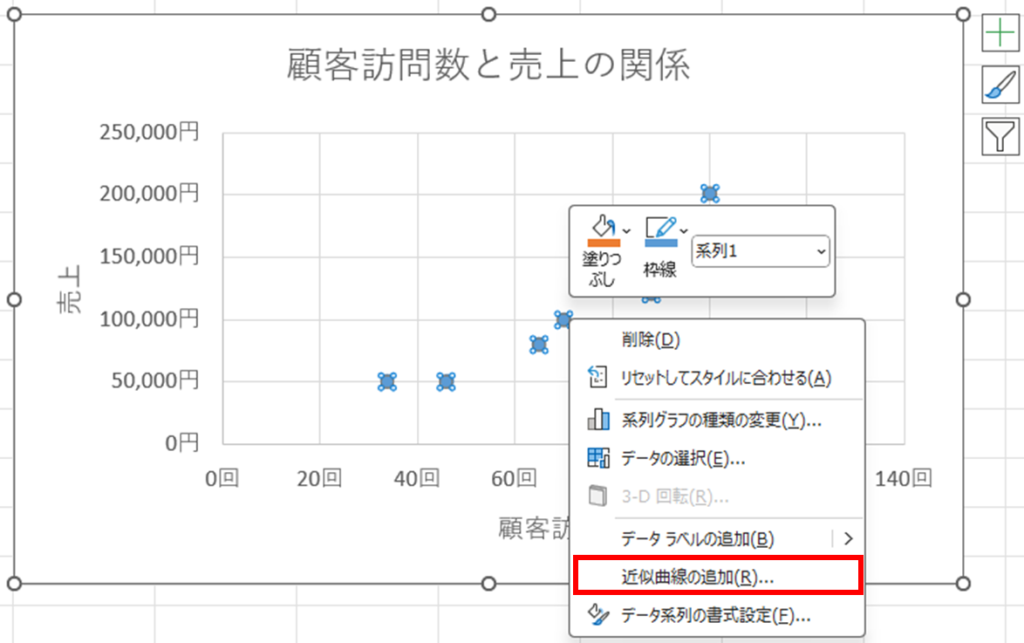
近似曲線の追加をクリックします。
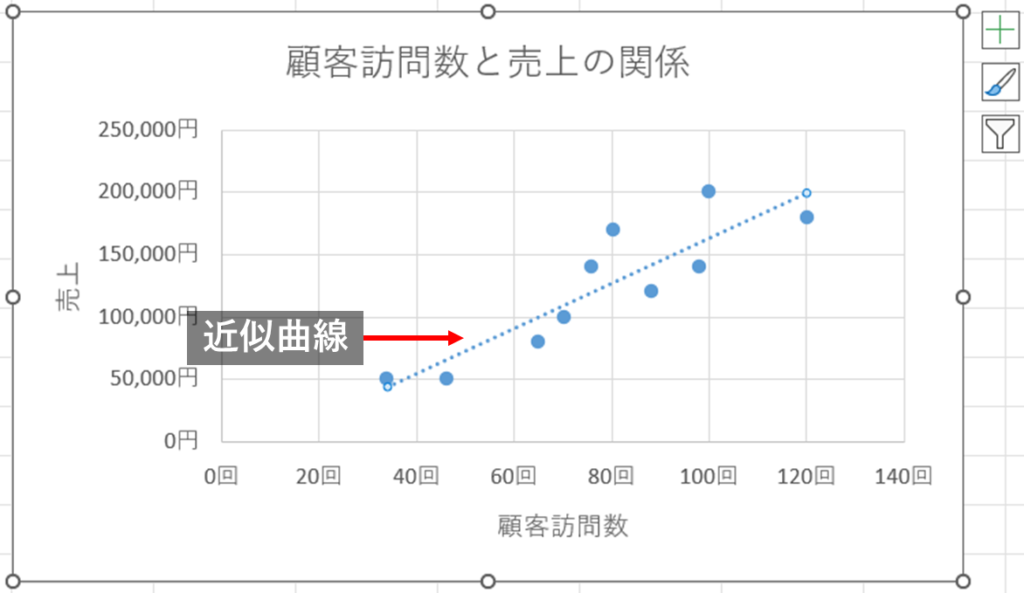
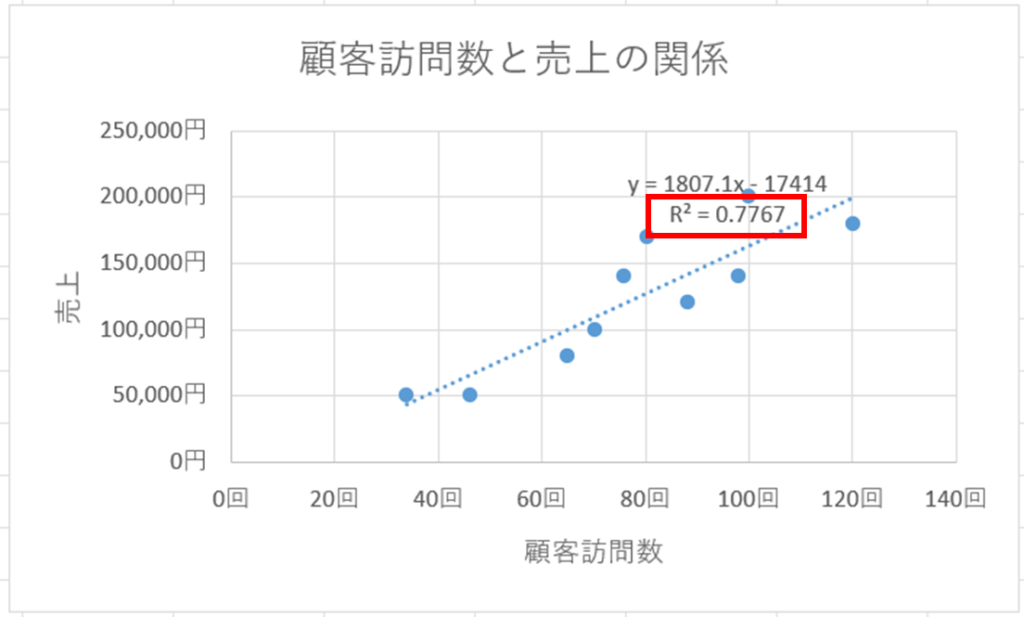
これで近似曲線を引くことができます。この近似曲線の周りにプロットされた点が集まっていると相関関係がより強いと言えます。こちらのデータでは点が近似曲線の近くにあり、比較的相関関係があると見えます。
数値での相関関係の検証
今度は、数値で相関関係があるかを検証します。相関関係は相関係数によって示すことができます。相関係数はCORREL関数を使って求めます。
| CORREL(配列1, 配列2) |
|---|
| 2つのデータセット間の相関係数を返す。相関係数は、2つの変数の間にどの程度の線形な関係があるかを示す指標で、-1から+1の間の値を持つ。 ・+1に近い：強い正の相関（一方の変数が増加すると、もう一方の変数も増加する傾向が強い） ・0に近い：弱い相関またはほとんど相関がない ・-1に近い：強い負の相関（一方の変数が増加すると、もう一方の変数は減少する傾向が強い） |
引数には、相関関係を求めたい2つの配列を選択します。ここでは、顧客訪問数と売上を選択します。
=CORREL(B3:B12,C3:C12)
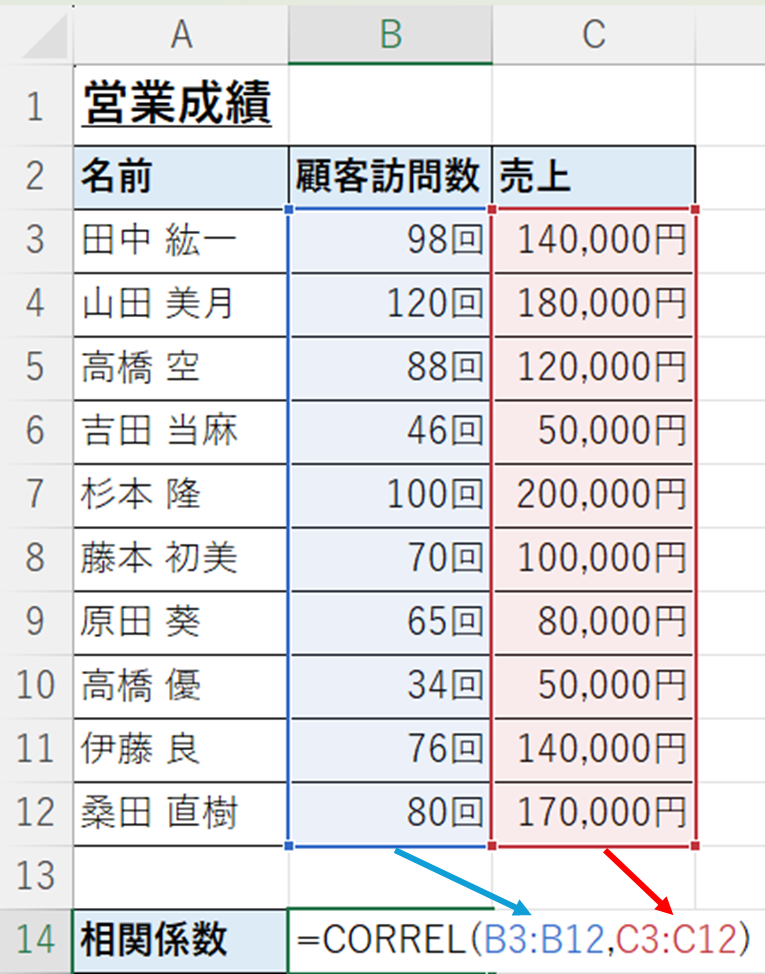
これで相関係数は0.88ぐらいとわかります。
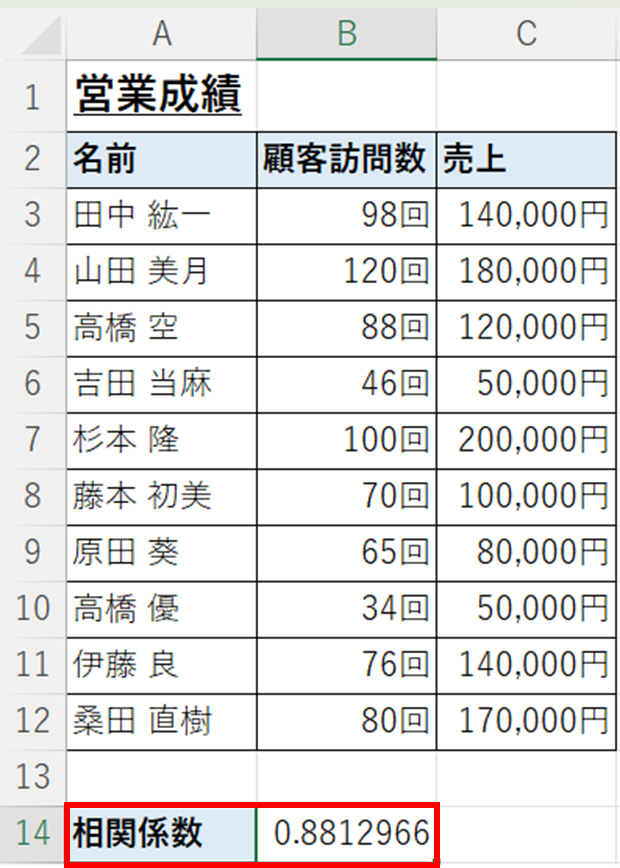
目安として相関係数が1~0.7であれば、強い相関があると判断できます。
－相関係数の目安－
0.7～ 1.0：強い相関
0.4 ～ 0.7：中程度の相関
0.2 ～ 0.4：弱い相関
0.0 ～ 0.2：ほとんど相関がない
結果、各担当者の顧客訪問数と売上には相関関係があると見てもよさそうです。
相関関係の傾向を把握
相関関係があるとわかったので、今度は、この傾向をより詳しく見ていきます。散布図上の近似曲線をクリックし、近似曲線のオプションを開きます。
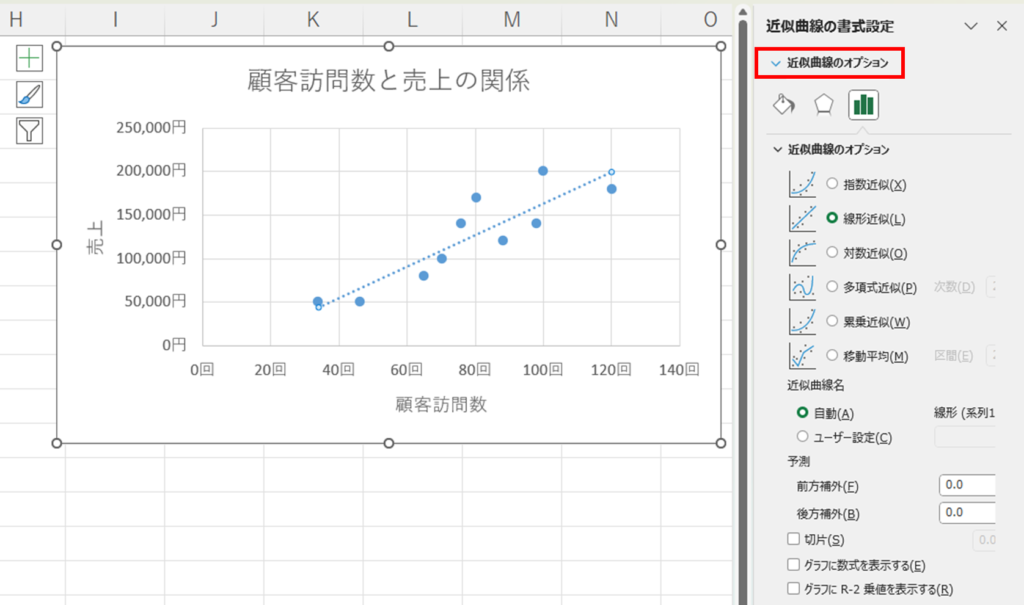
グラフに数式を表示するをクリックすれば、近似曲線の一次関数式が表示されます。
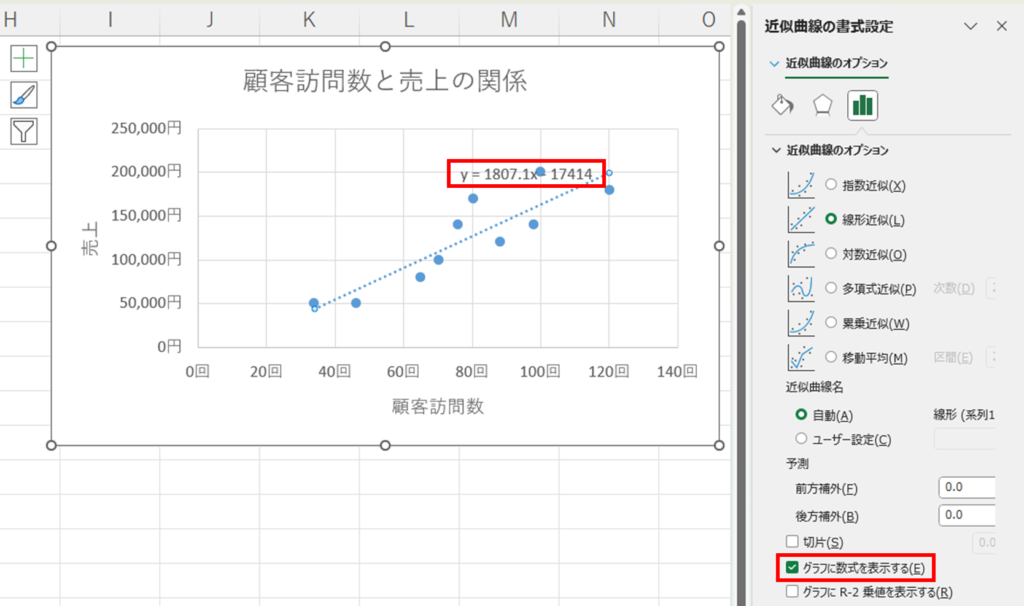
さらにグラフにR2乗値を表示するをクリックすれば、R2乗値が表示されます。
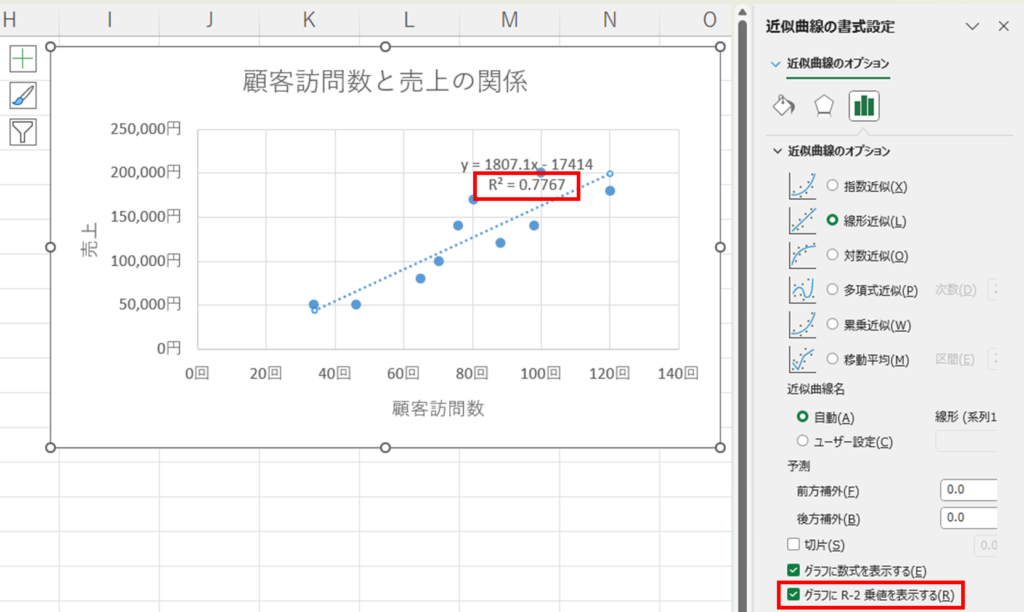
これは、決定係数を表し、近似曲線がデータの傾向をどの程度正確に表現しているかを示しています。1に近いほどモデルがデータの変動を非常によく説明できていると解釈されます。
| 決定係数の目安 |
|---|
| 0.8以上: モデルの当てはまりが非常に良い。データの変動の80%以上がモデルによって説明できる 0.6～0.8: モデルの当てはまりが良い 0.4～0.6: モデルの当てはまりは中程度 0.2～0.4: モデルの当てはまりは弱い 0.2未満: モデルの当てはまりは非常に弱い。このモデルで予測を行うのは適切ではない |
ここでは0.77ぐらいなので、比較的正確に近似曲線がデータの傾向を表していると言えます。
相関関係に基づき予測値・必要値を算出
今度はこの傾向から売上見込や目標を達成するための顧客訪問数を算出したいと思います。ここで、近似曲線の傾きと切片をそれぞれ求めたいと思います。
傾きはSLOPE関数を使って求めます。
| SLOPE(既知のy, 既知のx) |
|---|
| 近似曲線の傾きを計算する。傾きは、説明変数（x軸）が1単位変化したときに、目的変数（y軸）がどれだけ変化するかを示す。 |
1つ目の引数にY軸の売上高、2つ目の引数にX軸の顧客訪問数を選択します。
=SLOPE(C3:C12,B3:B12)
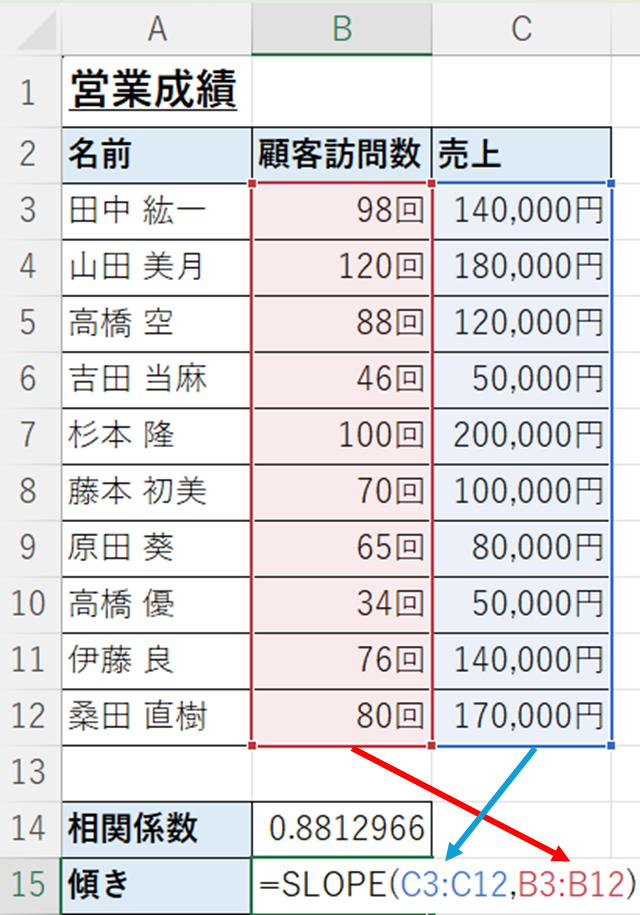
これで、グラフ上に表示されている式と同じ傾きの値を表示させることができます。
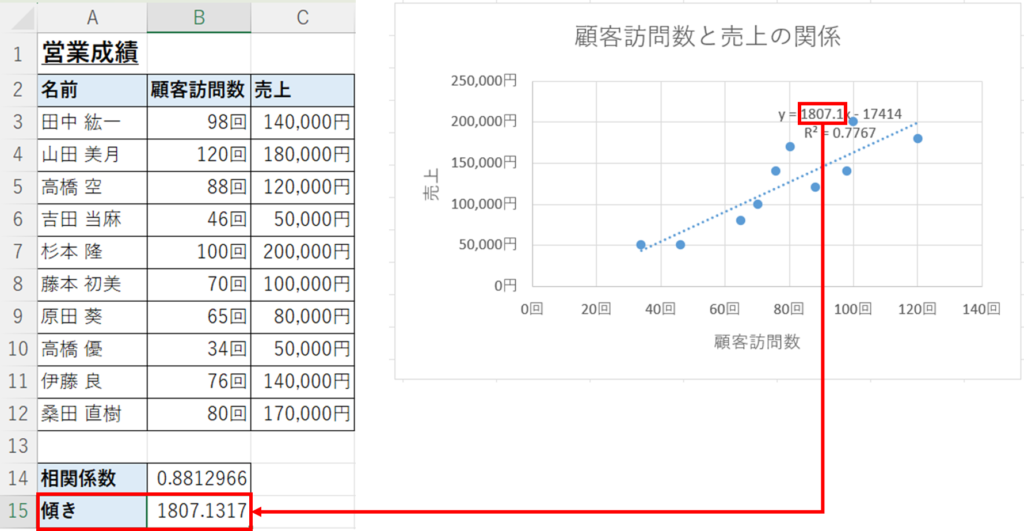
次に切片はINTERCEPT関数を使って算出します。
| INTERCEPT(既知のy, 既知のx) |
|---|
| 線形回帰直線の切片（y切片）を計算する。切片は、説明変数（x軸）が0のときの目的変数（y軸）の値を表す。 |
同じように1つ目の引数にY軸の売上高、2つ目の引数にX軸の顧客訪問数を選択します。
=INTERCEPT(C3:C12,B3:B12)
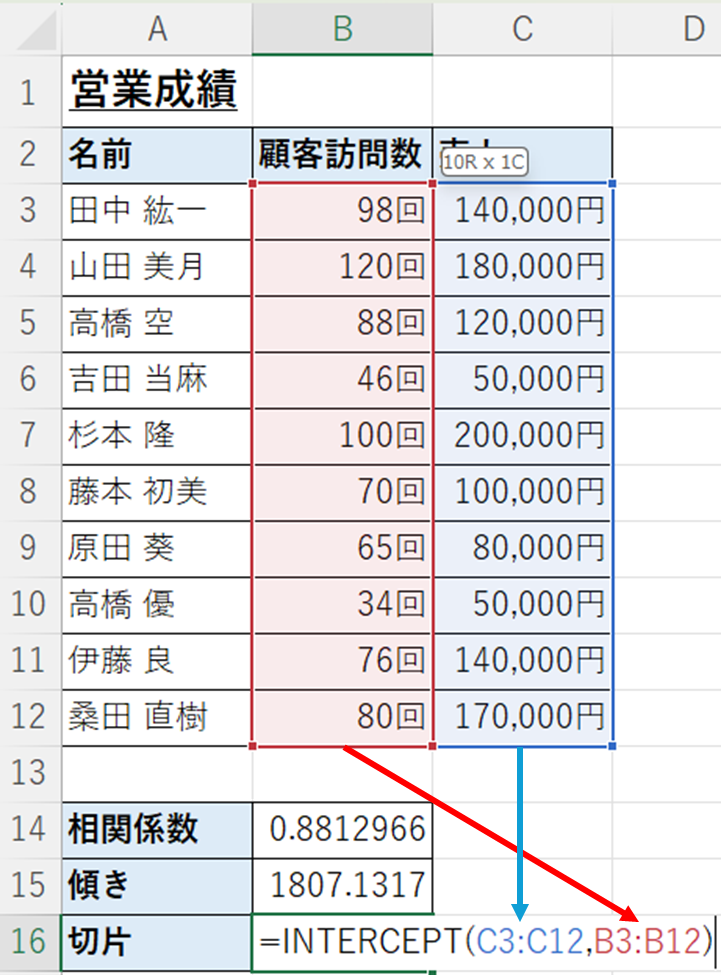
これで、グラフ上に表示されている式と同じ切片を表示させることができます。
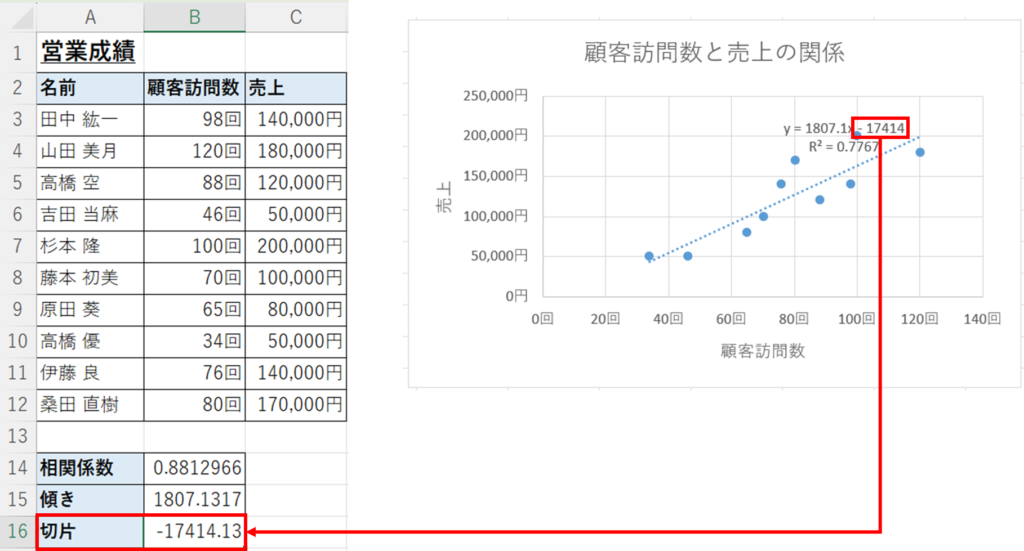
この傾きと切片を使って売上見込や目標を達成するための顧客訪問数を算出したいと思います。
顧客訪問数100回の場合の売上見込
まず、顧客訪問数100回の場合、どの程度の売上が見込まれるかを計算します。
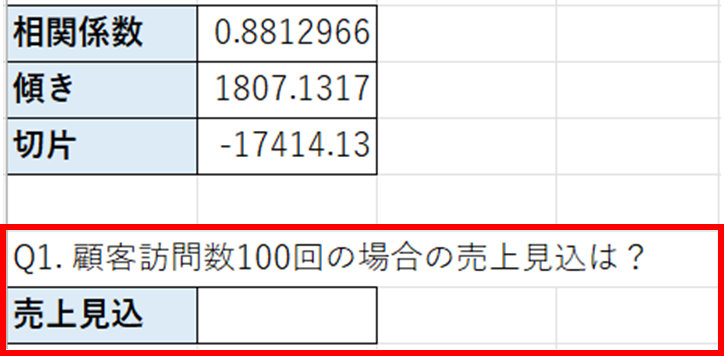
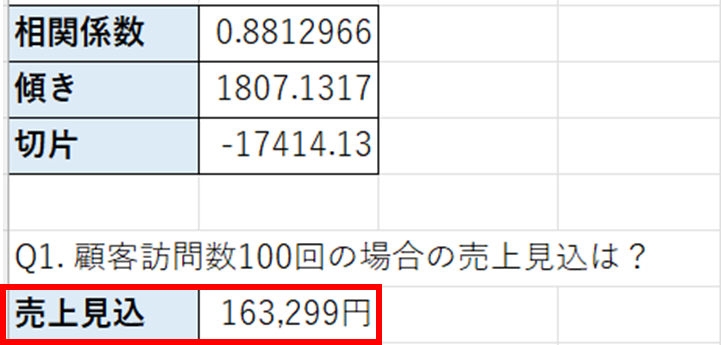
数式としては傾き×100+切片で計算します。これは、近似曲線の数式に代入し、yを求めています。
これで、100回訪問すれば16万3千円程度の売上が見込まれることが分かります。
売上20万円を達成するために必要な顧客訪問数
次に、売上20万円を達成するために必要な顧客訪問数を算出します。
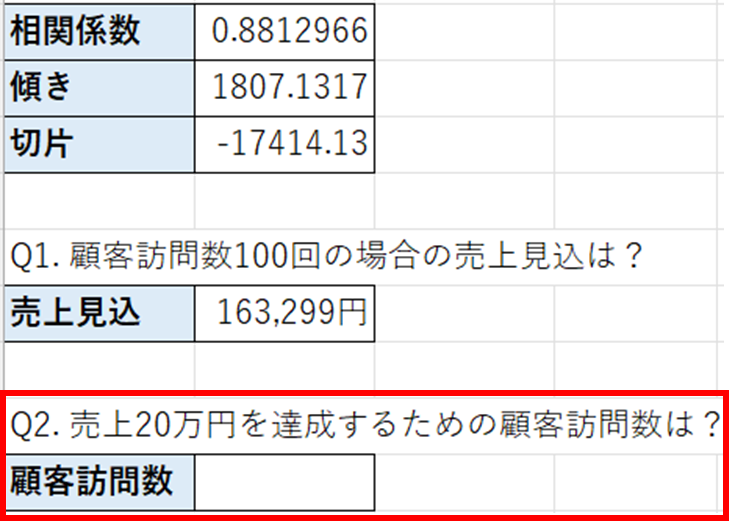
数式としては(20万-切片)/傾きで計算します。今後は近似曲線の数式に代入し、xを求めています。
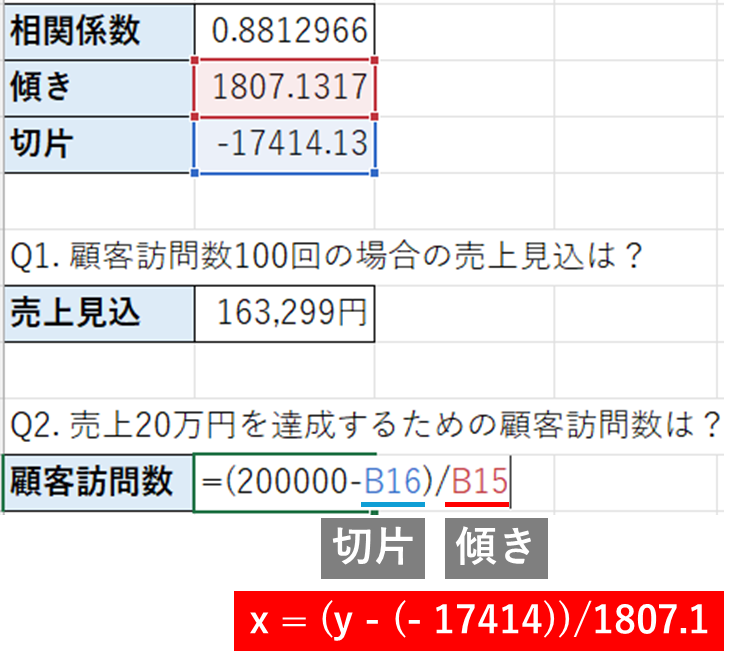
これで、売上20万円を達成するには120回程度必要になると予想することができます。
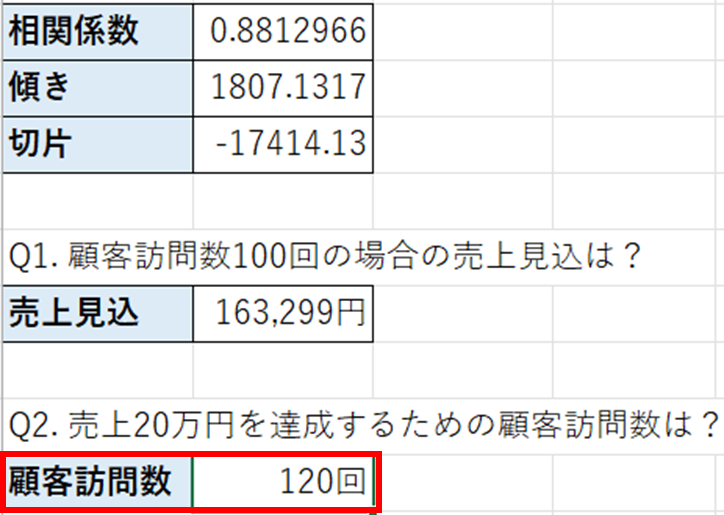
注意が必要なのは、こちらの結果はあくまで一般的な傾向に当てはめた場合の結果だということです。すごく優秀な人であれば、より少ない訪問数で目標売上を達成できるかもしれませんし、逆にもっと訪問数が必要な場合もあります。この点を踏まえて、数値を活用し、意思決定を行うことをおすすめします。
コメント