【Excel】 散布図を作成し、2つの数字の相関を調べる

本記事では、Excelで散布図を作成し、2つの数字の相関を調べる方法をご紹介します。

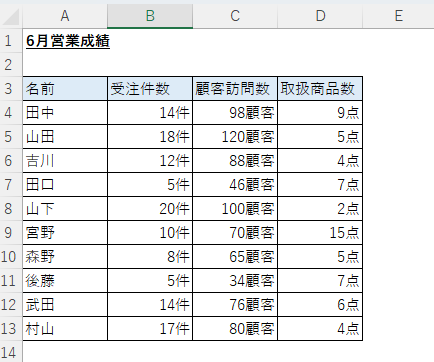
次のような営業成績を示す表があったとします。受注件数は顧客訪問数や取扱商品数に関係があるのではないかと考え、それぞれの数字に相関があるかを調べたいと考えています。

仮説

次のような仮説を検証したいと思います。

散布図を作成

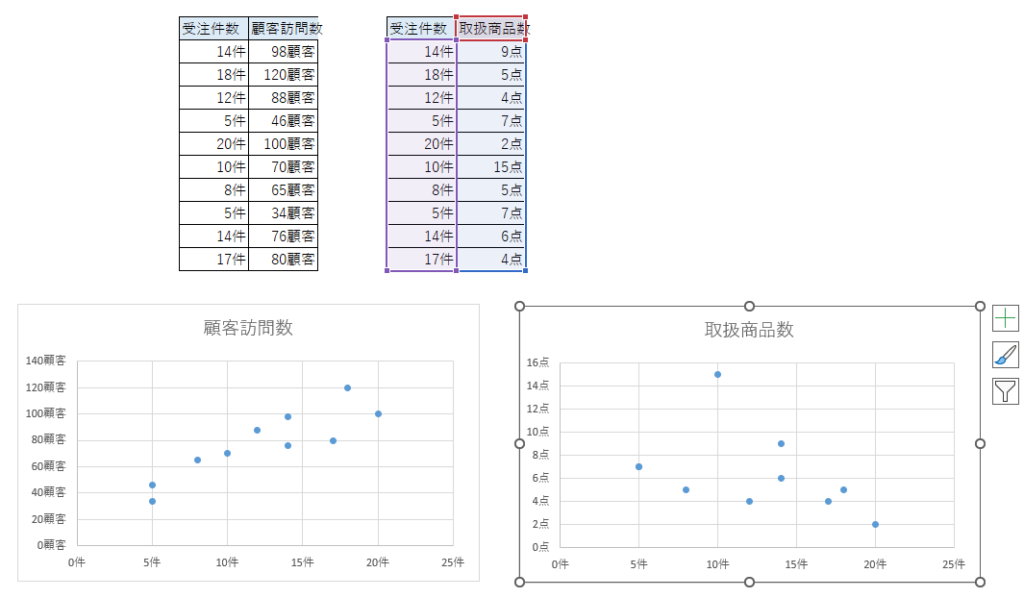
2つのデータの関係性を調べるために、「受注件数と顧客訪問数」、「受注件数と取扱商品数」の表を作成します。

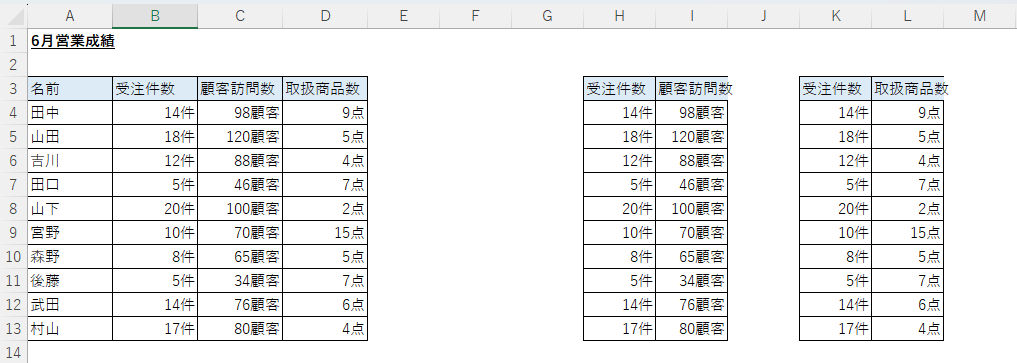
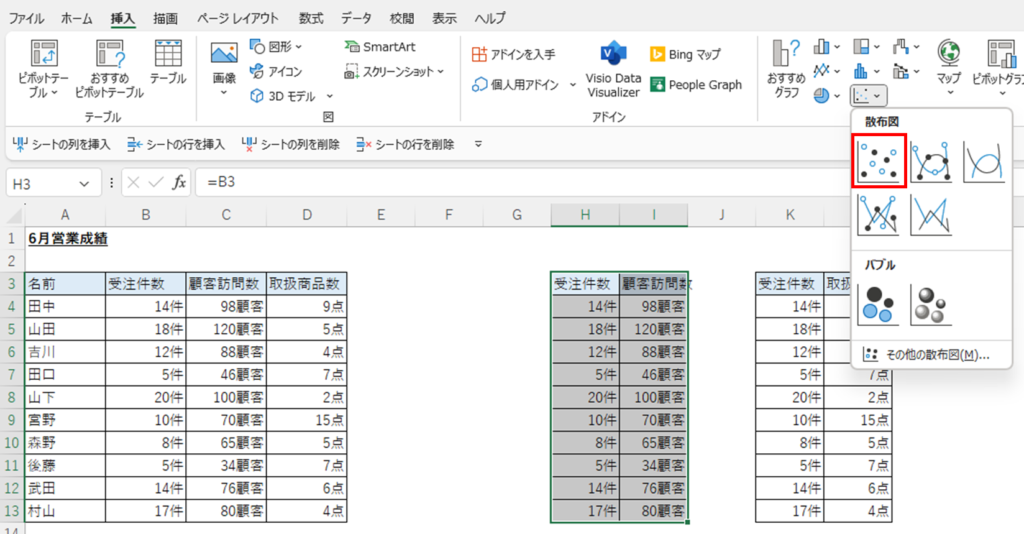
「受注件数と顧客訪問数」の表を作成し、「挿入」タブから「散布図」をクリックします。

するとこのようなグラフが表示されます。

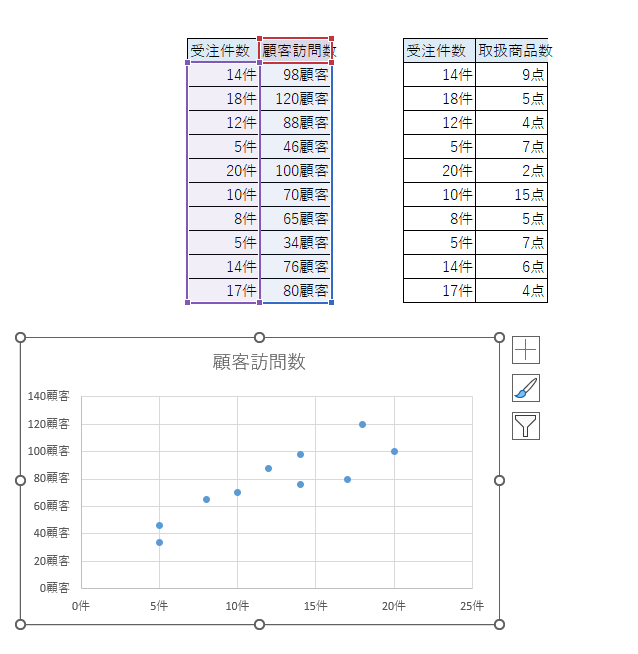
同様に「受注件数と取扱商品数」の表でも散布図を作成してみます。これだけ見ても何となく、受注件数と顧客訪問数の関係はありそうだけど、受注件数と取扱商品数の関係はなさそうに見えます。

相関を調べる

では、具体的なデータに基づき、相関があるかを検証したいと思います。

散布図の点を右クリックし、「近似曲線の追加」をクリックします。

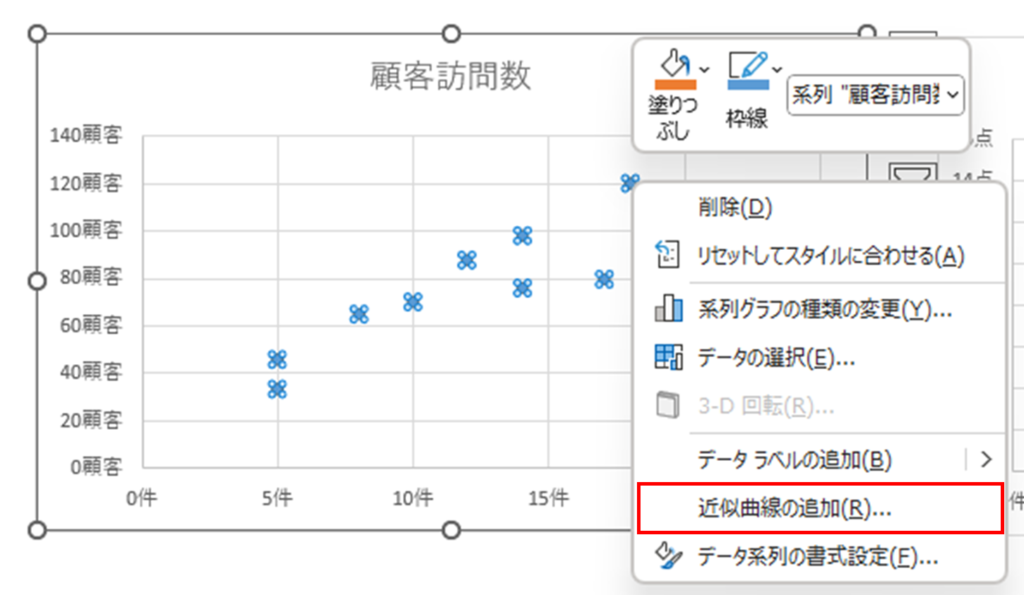
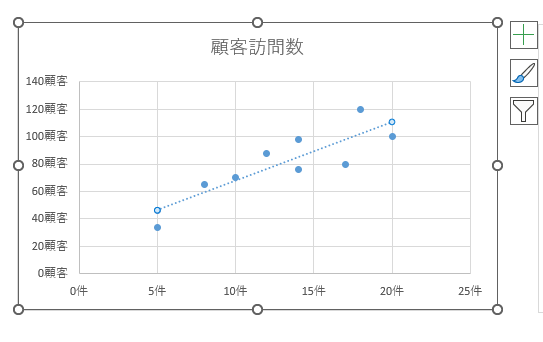
すると下図のような近似曲線が表示されます。

近似曲線は、散布図に示された点の真ん中を通る曲線のことを言います。散布図で示された点が、この近似曲線に集まっているほど相関があると判断できます。

それでは、具体的なデータを用いて相関を示したいと思います。

近似曲線を右クリックし、「近似曲線の書式設定」をクリックします。

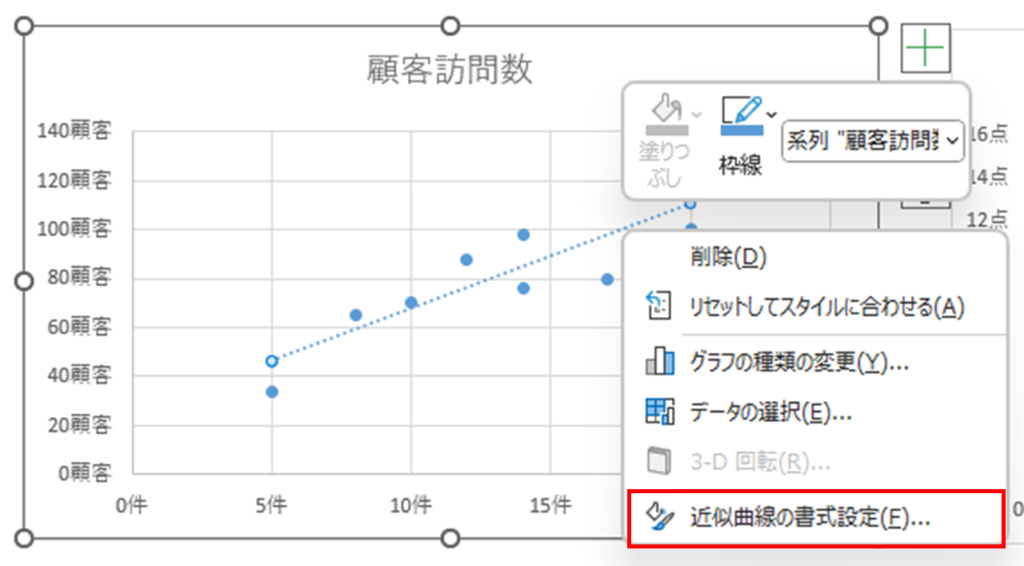
Excelの右側に書式設定画面が出るので、「グラフにR-2乗値を表示する」にチェックを付けます。

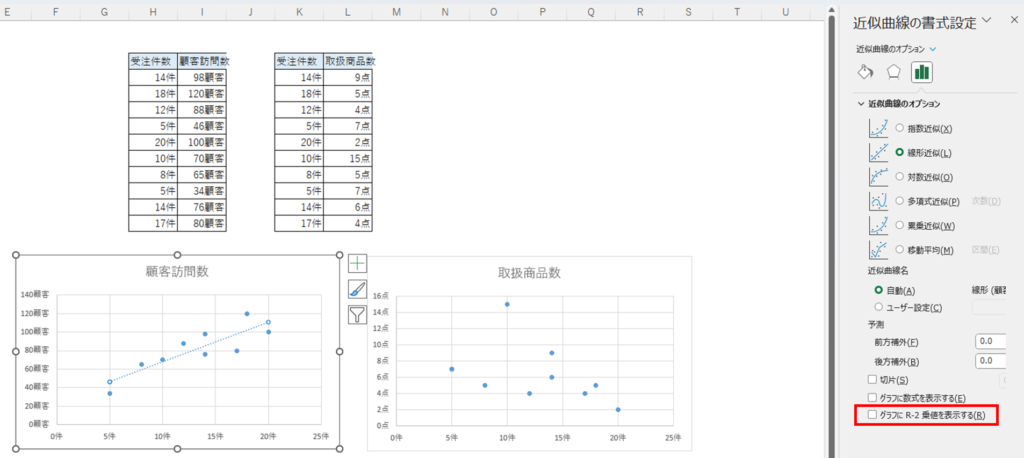
すると下図のようにR²の値が表示されます。

R²は決定係数といい、相関係数を二乗した値で、１から０の間をとる数値です。決定係数が１に近いほど相関があると判断できます。では、どれくらいの数値があれば相関があると判断できるかというと、絶対的な基準はありません。一般的には、0.5以上を目安に相関があるかないかを判断する場合が多いようですが、これもケースバイケースです。なので、他の数値と比較で相対的に判断するのが妥当かと思います。

同様に取扱商品数の決定係数R²を出してみます。

• 受注件数と顧客訪問数：R²＝0.7767
• 受注件数と取扱商品数：R²＝0.1741

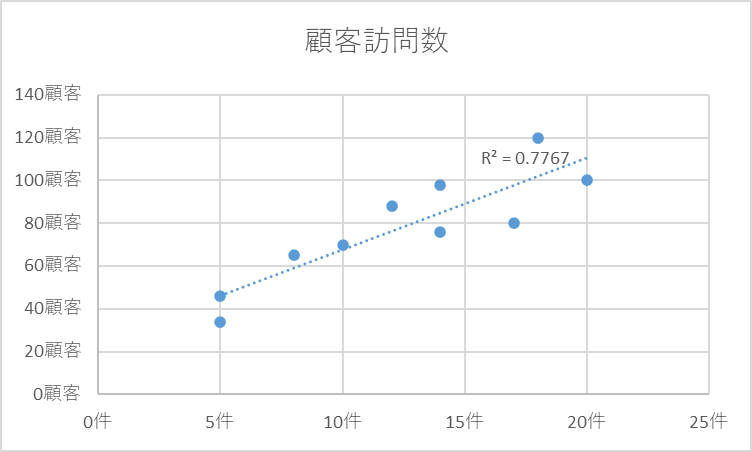
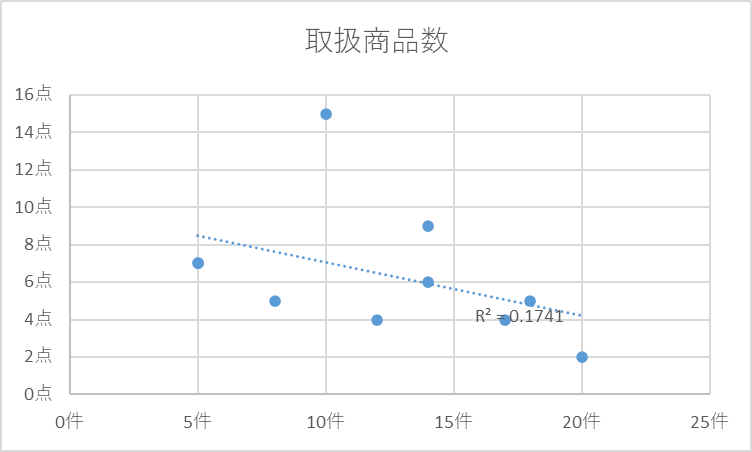
このデータによれば、受注件数は顧客訪問数との関係が強く、取扱商品数との関係は弱いと考えられます。

検証結果

上記のデータに基づくと、仮説は以下のように検証されます。